Non-Linear Systems

Non-linear dynamics are fascinating, if for no other reason than so many statistical models are linear, so testing for non-linearity often requires a more strong hypothetical foundation for understanding.

I'll discuss these topics in rough order of my personal favorites.

Oscillatory Dynamics

Oscillatory dynamics are the best. The most simple to understand is a pendulum, but you add a second pendulum to the end of the first and suddenly the non-linearities lead to some crazy complexities.

Check it out:

I love this because oscillations play an important role in neural communication, perception, etc. This is the focus of my neuroscience research and is, of course, the name of my scientific blog, Oscillatory Thoughts..

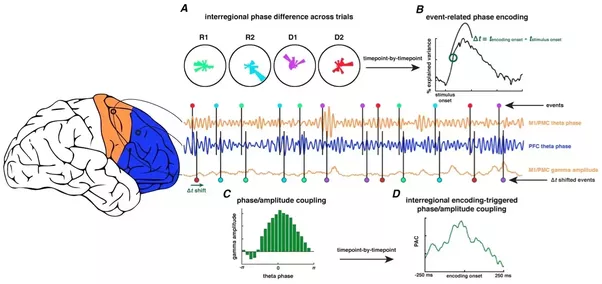
This is a figure from a paper of mine currently under review, for example, showing a model wherein neuronal oscillations coordinate communication between brain regions. This is nice because it allows for "cleaner" communication in a noisy environment (think about a radio):

Resonance

Closely related to oscillatory effects, but can be nice to demonstrate certain emergence effects, in contrast to some of the chaotic effects of other non-linear systems. Check out this simple demonstration of resonance and emergence:

Simulating 10^6 neurons sending signals to one another can also lead to interesting emergent "waves" of activity caused by the non-linearities of the interneuronal communication effects:

Power Laws

Social networks are so hot right now. Social networks follow a power law (aka the six degrees of Kevin Bacon effect). Some people (influencers) know a lot of people, whereas most people know relatively few. This is the infamous "black swan" "long tail" effect.

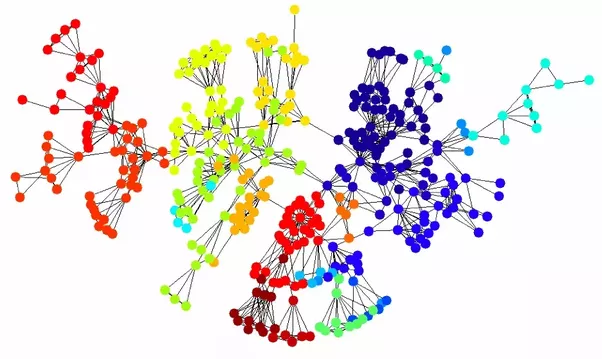
Without getting into too many details, power laws are "scale-free" in that they have no preferred length scale. This (roughly) means you can "zoom in" on any portion and retain the original complexity. By definition, this is a fundamental feature of fractals.

I find fractals and power laws super interesting not only because of how prevalent they are in neuroscience, but also their real world consequences are fascinating. The classic example is the question of How Long Is the Coast of Britain?

The famous Zipf's Law is a power law distribution concerning word frequency. Some words appear a lot in language, while many words are very infrequently used. Here's a plot of the English language Wikipedia's word frequency:

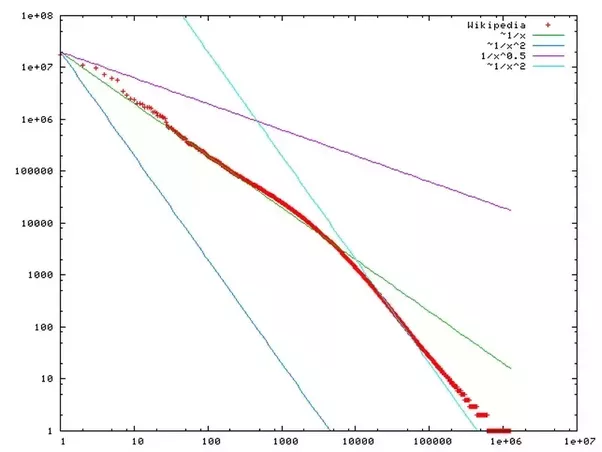
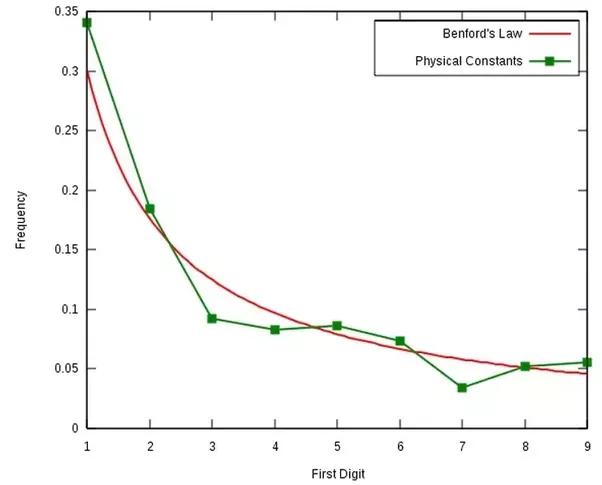
Another power law that's received a lot of attention is Benford's Law, which states that the distribution of digits in a lot of data are not even, but power law distributed. For example, in base 10, the number one should, all things being equal, appear 10% of the time. But in many data sources one appears around 30% of the time. This fact is actually used to help detect fraud in, for example, tax returns.

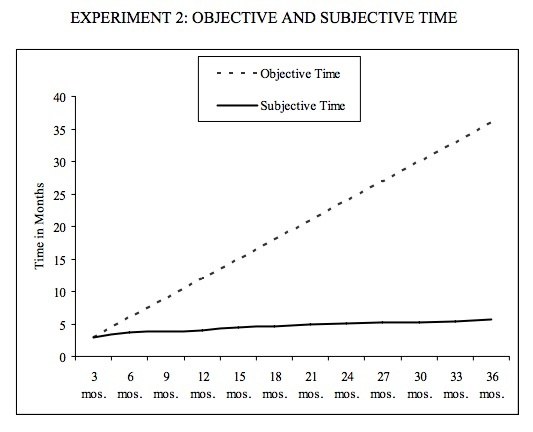
One of my favorite answers on Quora, that by Michael Wolfe to Engineering Management: Why are software development task estimations regularly off by a factor of 2-3?, embodies power laws in human perception very nicely. We tend to subjectively experience time as the logof objective, actual time. Meaning we're really really bad at estimating how long something took, or how much time has passed. Check out the results from this paper.

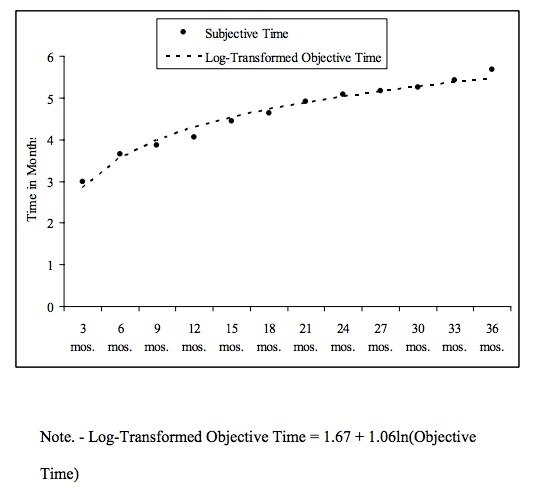
In the words of the authors, "subjective estimates of future time horizon change less than the corresponding change in objective time." Here's the same data, but log-transformed to highlight the power law effect:

U-shaped curves

These are ubiquitous in learning, economics, and pharmacology. The classic is the Kuznets curve.

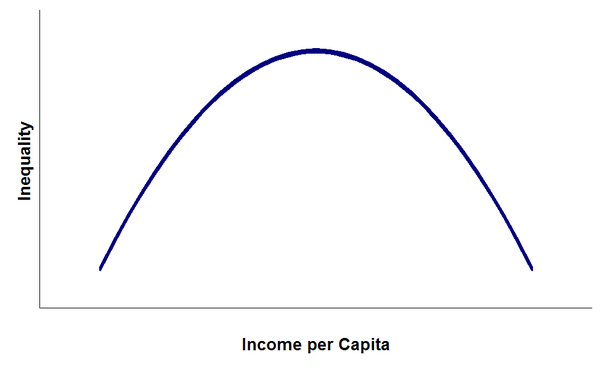
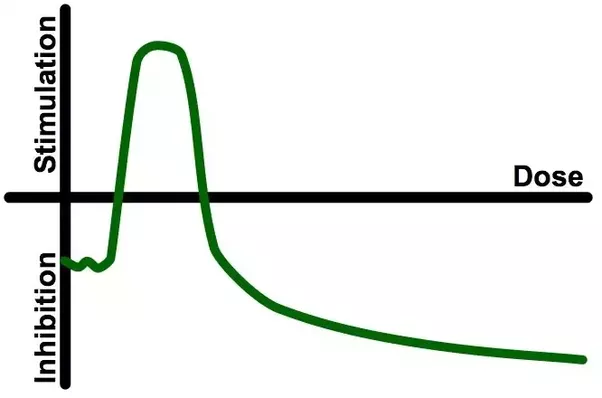
U-shaped (or inverted U-shaped curves, such as the one above) are also highly prevalent in pharmacology. This is captured by the idea of Hormesis, "It is conjectured that low doses of toxins or other stressors might activate the repair mechanisms of the body. The repair process fixes not only the damage caused by the toxin, but also other low-level damage that might have accumulated before without triggering the repair mechanism."

Other non-linearities

Non-linear relationships can be modelled using any number of non-linear equations. For example, I've got data that suggests that cognitive slowing increases not as a linear function of age, but rather it accelerates with age.

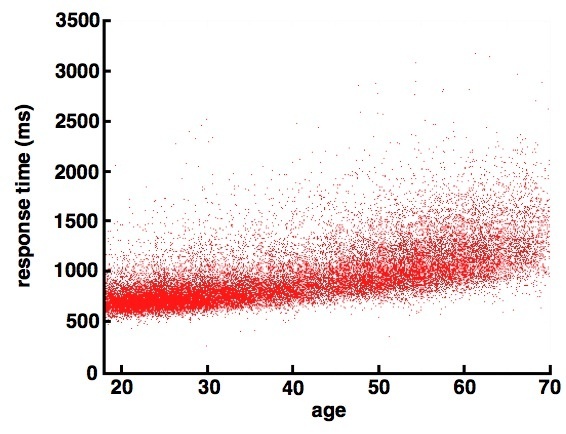
To paraphrase Dr. Ian Malcolm, non-linear systems are, uhhh, awesome.

(This post originally appeared on my blog, Oscillatory Thoughts and was inspired by a question over on Quora.)